يعد كتاب 1000 لعبة تفكير: ألغاز، ومفارقات، وخدع، وألعاب من أفضل الكتب التي تساعد الطفل على تنمية مستوى الذكاء والتفكير لديه، حيث ينقسم الكتاب إلى عدة فصول يركز كل منها على جانب معين ومهارة محددة لإثراء وتحفيز عقلية الأطفال ليكونوا أكثر إبداعا ومنهجية علمية، حيث سيجدون فيه التنوع بين الألغاز والأحاجي والألعاب العقلية. كما يجب ألا نغفل جانب المتعة أيضا والتي تدفعهم للتعلم واكتساب أدوات التحليل والاستنتاج والمهارات، مما سينعكس على تفكيرهم وإدراكهم.
يمكنك مشاهدة آراء القراء على موقع جودريدز من خلال الرابط التالي:
طلب شراء كتاب 1000 لعبة تفكير
يمكنك طلب شراء النسخة الأصلية من كتاب 1000Playthinks: Puzzles, Paradoxes, Illusions & Games من موقع أمازون من خلال هذا الرابط:
طريقة استخدام كتاب 1000 لعبة تفكير: ألغاز، ومفارقات، وخدع، وألعاب
صممت ألعاب التفكير في كتاب 1000 لعبة تفكير لكي تسمح للطفل بالوصول إلى العديد من الأفكار بطريقة سهلة ومن خلال السياقات المتنوعة وبمستويات مختلفة. لقد صنفت كل لعبة من ألعاب التفكير وفقا لمستوى الصعوبة من 1 وحتى المستوى 10، ويمكنك العثور على الألغاز التي تناسب مستواك، تحقق من المؤشر الموجود في نهاية الكتاب.
يمكنك أيضا التنقل في الكتاب أولا من خلال اختيارك الألعاب التي تهمك أكثر من غيرها. أو يمكنك استخدام المفاتيح الموجودة في الجزء العلوي من كل لغز من هذه الألغاز بوصفه دليلا لك. تستطيع أيضا القيام ببعض الأنشطة منفردا وذلك في الأنشطة الفردية، أو تأتي بمجموعة من الألعاب والألغاز الجماعية عندما تكون مع أحد الأصدقاء.
ملخص كتاب 1000 Playthinks
التفكير في ألعاب التفكير
“الخيال أكثر أهمية من المعرفة”.
ألبرت أينشتاين
ومن الألعاب الموجودة في هذا الفصل من كتاب 1000 لعبة تفكير: ألغاز، ومفارقات، وخدع، وألعاب نجد التالي:
هل تستطيع أن تثبت أن السبعة نصف الاثنى عشر؟
- 7 + 7 = 12 ؟
هل تستطيع الإجابة عن السؤال القديم: أيهما جاء أولا البيضة أم الدجاجة؟
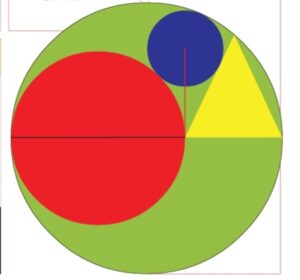
مسألة سانغاكو (sangaku) منذ عام 1803 م.
على قطر الدائرة الخضراء الكبيرة، ضع مثلثا متساوي الساقين ودائرة حمراء صغيرة، بحيث تكون قاعدة المثلث منطبقة على قطر الدائرة الكبيرة، وأما الدائرة الصغيرة فتوضع بحيث تلامس محيط الدائرة الكبيرة، ويمتد قطرها عبر قطر الدائرة الكبيرة المارة بقاعدة المثلث. الآن أضف دائرة ثالثة وارسمها بحيث تلمس الدائرتين الأخريين والمثلث. فإذا رسمت خطا من مركز الدائرة الثالثة إلى نقطة تلامس الدائرة الحمراء مع المثلث، فهل تستطيع أن تثبت أن هذا الخط في الواقع عمودي على قطر الدائرة الخضراء الكبيرة؟
هل هناك طريقة ما لاستخدام الرقم 6 ثلاث مرات ليكون الناتج الرقم 7 ؟
هل تستطيع عمل ثقب في البطاقة البريدية بحيث يكون كبيرا بما يكفي ليعبر رجل من خلاله؟
علم الهندسة
“إنني أمتلك قدرة ضعيفة وسيئة فيما يتعلق بتصور العلاقات، وهذا الأمر جعل دراسة علم الهندسة وجميع المواضيع المنبثقة منه مستحيلة الفهم بالنسبة إلي”.
سيجموند فرويد
ومن ألعاب هذا الفصل نجد التالي:
- هل يمكنك أن تتصور ومن ثم ترسم مجسما ذا شكل دائري ومثلثا ومربعا في آن واحد؟
- في الهندسة الإقليدية يوجد للمربعات شكل واحد فقط. هل تنطبق هذه القاعدة على هندسة سيارة الأجرة؟
- سوف يبكي هذان الطفلان في الصفحتين المتقابلتين حتى يتمكنا من اللعب معا. كيف تستطيع أن تجعلهما سعيدين من دون أن تبعد أحدهما عن مهده أو أن تبعد الآخر عن الكرسي؟

- المكعب له تناظرات دورانية أكثر من تلك التي للشكل ثنائي الأبعاد. هل تستطيع أن تجدها كلها؟
النقاط والخطوط
- من خلال ثلاثة خطوط تستطيع عمل مثلث واحد، ومن خلال أربعة خطوط تستطيع عمل أربعة مثلثات. من خلال إضافة خطين مستقيمين آخرين للخطوط الثلاثة الموضحة هنا؟
- هل تستطيع قطع قرص من الجبن إلى ثماني قطع متماثلة بثلاث عمليات قطع مستقيمة؟
- خمس عمليات قطع مستقيمة كافية لتقطيع الكعكة إلى خمسة عشر قطعة. هل يمكنك تقطيع الكعكة إلى ست عشرة قطعة عن طريق خمس عمليات قطع فقط؟
- ارسم أربعة خطوط مستقيمة فقط عبر محيط الدائرة. هل تستطيع فصل هذه الخنافس (الدعسوقات) الإحدى عشر لتصبح كل واحدة منها في منطقة وحدها؟

- هل تستطيع ربط تسع نقاط بأربعة خطوط مستقيمة من دون رفع قلم الرصاص عن الورقة؟ وهل تستطيع حل هذه المسألة باستخدام ثلاثة خطوط مستقيمة فقط؟
الرسوم البيانية والشبكات
- ما عدد الطرق المختلفة التي تستطيع عن طريقها وضع ستة أسهم على وجوه المكعب؟
- هل تستطيع تحديد اتجاه الأسهم الأربعة المفقودة؟

- تزحف الدودة فقط بمحاذاة حواف صندوق أبعاده 2 سم، 2 سم، 3 سم. فما أطول مسافة تستطيع الدودة أن تقطعها من دون أن تكرر في أي مسار سبق لها السير فيه؟
- توجد تسع عشرة حبة من الخرز على المنضدة. هل تستطيع ربطها بخيط لعمل رسم بياني شجري؟
- ما أصغر عدد من الفروع يمكنك رسمه بين التسع عشرة حبة من الخرز، أو التسع عشرة نقطة؟ تذكر أن كونه رسما بيانيا واحدا، فلابد أن ترتبط كل نقطة بالنقاط الأخرى كلها عن طريق عدد من الفروع. ولأنها رسم بياني شجري فلا يمكن أن تكون هناك حلقات مغلقة. هل توجد قاعدة عامة لتحديد أقل عدد من الفروع اللازمة؟
المنحنيات والدوائر
ومن أمثلة الألعاب الموجودة في هذا الجزء من كتاب 1000 لعبة تفكير: ألغاز، ومفارقات، وخدع، وألعاب نجد التالي
- لماذا تكون أغطية الحفر مستديرة؟ هل تستطيع العثور على ثلاثة أسباب لكون الشكل المستدير هو أفضل شكل ممكن؟ مع العلم أن الإجابة (لأن الحفر مستديرة) لا تؤخذ في الحسبان.
- توجد خمس نقاط موزعة عشوائيا على محيط دائرة. مبتدئا بأي نقطة منها، هل يمكن رسم خط يربط النقاط الأخرى على صورة مضلع قبل العودة إلى نقطة البداية؟
- وما عدد المضلعات المختلفة التي يمكن رسمها بهذه النقاط الخمس؟
- هل تستطيع ترتيب ست عشرة عملة معدنية مسطحة على منضدة، بحيث تلامس كل قطعة ثلاث عملات نقدية أخرى فقط؟ يجب أن تكون القطع النقدية كلها في وضع مستوٍ وغير متداخلة.
- هل تستطيع وضع أنصاف الدوائر الثمانية على خط الاوتاد ذي النقاط السوداء في الأسفل، بحيث لا يتقاطع أي من أنصاف الدوائر، وأن يكون هناك وتد عند كل طرف من طرفي كل نصف دائرة؟ علما بأنه يسمح بتوزيع أنصاف الدوائر على جانبي خط الأوتاد، ولا يسمح بتشارك أي نصفي دائرتين في أي وتد.

الأشكال والمضلعات
من خلال هذه الأشكال الهندسية أجب عن الأسئلة التالية:

- كم عدد المثلثات في الشكل رقم 1؟
- وكم عدد المثلثات في الشكل رقم 2؟
- كم عدد المثلثات والمربعات في الشكل رقم 3؟
- في الشكل رقم 4 كم عدد المربعات؟
- كم عدد المثلثات في الشكل رقم 5؟
- وكم عدد المثلثات والمربعات في الشكل رقم 6؟
- كم عدد الأشكال السداسية المنتظمة في الشكل رقم 7؟
- في الشكل رقم 8 كم عدد المربعات؟
- وأخيرا كم عدد المربعات في الشكل رقم 9؟
إذا كان كل مربع صغير بين أربعة أوتاد يشكل وحدة مربعة واحدة، فكم المساحة المحصورة من قبل كل مضلع من مضلعات لوحة الأوتاد المرقمة من 1 إلى 16؟

ولا يزال هناك الكثير من ألعاب التفكير الموجودة بكتاب 1000 لعبة تفكير، حيث يوجد ألعاب على الأنماط، والتقسيم لأجزاء، والأعداد، والمنطق والاحتمالات، والطوبولوجيا، والعلوم، والإدراك، سأترك لكم المجال لتكتشفوها بأنفسكم.
وصف كتاب 1000 لعبة تفكير
| اسم الكتاب | 1000 لعبة تفكير: ألغاز، ومفارقات، وخدع، وألعاب |
| تأليف | إيفان موسكوفيتش |
| ترجمة | عبدالعليم يوسف أحمد محمد |
| مراجعة | بدر بن عبدالرحمن بن حمد البسام |
| دار النشر | مدينة الملك عبدالعزيز للعلوم والتقنية KACST |
| عدد الصفحات | 432 صفحة |
وفي النهاية، لا تنسى أن تقوم بمتابعتنا أيضا على منصات التواصل الاجتماعي:




